Now Loading..

It's a Wonderful World!

Last updated 2024- 9-16, 1:16:48 P.M. UTC+00:00

Various noteworthy bits

About this page

I plan on keeping this page updated with various bits that pop up now and then.

Video-related

AE Iceberg

Motion math, Pixel Bender, Brainstorm, Artisan, $ object in expressions, the audio effects, Photoshop 3D layers respond to AE cameras, and the list goes on. What happened to UXP?

Raster Stroke Effects in AE

The bottom row shows what happens if you enable motion blur.

Raster Stroke FX Compo

Rule I

(Rule I of otoMAD Collabs) There is always a part whose visual organization is based on comic book or manga panels.

AE: Solids vs Shapes

Shape layers inherit from AVLayer, while Solids are FootageSource. This means you can directly use the replace feature to replace actual footage onto solids but not with shape layers. So there is a difference between using a big rectangle shape and using a solid layer.

AE Lisp Expressions

Once upon a time, I wrote a Lisp interpretor in JS. It works for AE expressions. You can find it here.

The Good Ending.#lisp #aftereffects pic.twitter.com/3YCJzy1pEh

— lachrymaL (@lachrymaL_F) November 19, 2021

OtoMAD/YTPMV/... is merely ostensibly niche

It is a commonly expressed viewpoint among those in my circle that otoMAD/YTPMV mediums are of a small audience on the world wide web. But this doesn't seem to universally be the case.

First and foremost it is important to realize that these videos don't always carry the names with which you may be familiar (reminiscent of some not being able to recognize kanji leadding to confusion of MADs with otoMADs). In Japan, otoMADs and otoMAD-like content have consistently been present in the general collective online consciousness (also due in part to the popularity of various source materials carried within the medium). They have made their way into the real world in observable ways, such as various television adverts employing the styles of the Tom Brown series popular on NicoNico.

In China especially, it is quite difficult to meet someone online under the age of 25 who is not aware of so-called Guichu (鬼畜) videos, which are essentially indistuiguishable from (in fact, its origins cannot be separated from) what is known as otoMAD outside of China. There is some interesting (and, at times, quite dark) history surrounding the development of this genre of videos in relation to the Chinese otoMAD scene. Here are some English sources which can serve as a survey for those who are interested: 1, 2. Further, there is some academic discussion in China studying the social phenonmenon related to Guichu videos and, of course, some find the need to mention otoMADs. Similar papers exist in Japan about online media and otoMADs.

Recently there has been a lot of discourse in the Japanese and Chinese circles on the question of what OtoMAD really is. We see the difficulty in defining this term: In recent years it is increasingly clear how much the videos tagged with OtoMAD have departed from those made at the inception of the term. Let's ask ourselves some questions as a thought experiment: Does an OtoMAD require some sort of visual simulacra? Then, does an OtoMAD require some sort of audio simulacra? If so, must it have pitch shifting, or must it have sentence mixing? Can you get past with not manipulating anything? Do you need rhythm?

I know that everyone has their own answers to this set of questions, but I personally already feel overwhelmed with all the nuance that any informed individual can bring to the table. Coming up with a encompassing definition indeed seems like an impossible feat.

I believe I have heard that 2÷す had mentioned that, by recording his journey to the convenience store to pick up some beers, he is effectively making an otoMAD of 4′33″ (John Cage). FFFanwen has posited a theory of "infinite expansion" around what the word "otoMAD" can refer to (relatively specific to the context of Chinese circles, due to its unique history in part related to Guichu), which culminates in the thesis that "we shall not define what it is, as any definition will influence our perception of its potential".

So far this issue has been discussed in a descriptivist tone, that is, we consider anything that has the chracteristics of an OtoMAD (whatever definition that may entail), an OtoMAD (see more about this here). Perhaps we should be more perscriptivist from the perspective of the author, which is more simple: The work is an otomad if and only if the author says so. But this has its own issues, for example, how do we determine authorship? To what degree do you need to participate in the creation to be considered an author? Did your "source material" have a say in this? Do you even need any "source material" (whatever the definition may be)? (In other words, is the OtoMAD medium fundamentally derivative of other works?) There are bigger questions about artistic authorship that are still debated in academia today; it seems rather short-sighted to pin anything down firmly in place.

Tianxiang Li, remarked recently that there is a sort of "convergent evolution" at play: OtoMADs (which came from MADs), Guichu (which is associated usually with some sense of mockery or parody), and YTPMV (which is really about sampling in the EDM sense), are all materially indistuiguishable, yet, coexist, for reasons that are seemingly distinct. It seems quite natural to clump these together into the same category, which, is how the word "OtoMAD" is starting to be used in some circles. Yet, we seem to be in somewhat of a "Dark Forest" situation, where distinct communities that are not qualitatively different refuse to make contact with each other (in part due to the notorious close-mindedness of some).

Specifying Frame Number on ImageTexture (Blender)

You can do this in Geometry Nodes. However this is not available in Shader Nodes. If what you are doing is procedural you can check this out. There are other ways to get around this. One of them being stitching all the frames into one big image texture, then control the transform vector with care and precision. The other way is to use UDIMs.

Dear ImGui vs. AE

This is completely psychotic. I cannot believe someone would do this.

Jinriki Vocaloid

You can read more about this on VocaDB here. A couple years back there was a certain part in an otoMAD collab that had vocals so insane that I'd solemnly declared it's the best I've ever heard. The character was even singing in a different language from its source material. It turns out those were actually recorded by a commissioned vocalist. But I'm sure Getsuren(名残雪)-senpai would never betray me like this.

Rule II

(Rule II of otoMAD Collabs) There is always a transition from/into some sort of screen (TV/monitor).

Justin Frankel vs. YTPMV

If you don't know, he's usually associated with Winamp and REAPER. For his reaction to this particular use case of REAPER, see here.

BlendView

Blender-to-AE bridge similar to CINEWARE. I'm unsure what happened to this project.

Convolution

Since raster images are discrete pixels, convolution in image processing refers specifically to discrete convolution. We set out to define \(F\) to be the matrix of pixels for an image, then \(F_{x, y}\) specifies the color of the image at position \((x, y)\). Then define some small square matrix \(G\) with the size of an odd number \(D\). Then define the center of the matrix \(G\) to be the "origin", and set to start the sum at the origin from \(-\delta\) to \(\delta\) where \(\delta = \lfloor \frac{D}{2} \rfloor\).

$$(F \ast G)_{x, y} = \sum_{n=-\delta}^{\delta} \sum_{m=-\delta}^{\delta} {F}_{(x + n) \times (y + m)} \cdot {G}_{n \times m}$$

The \(G\) is called the kernel. Different choices for this matrix will result in different effects, such as Box Blur, Gaussian Blur, Find Edges, etc.

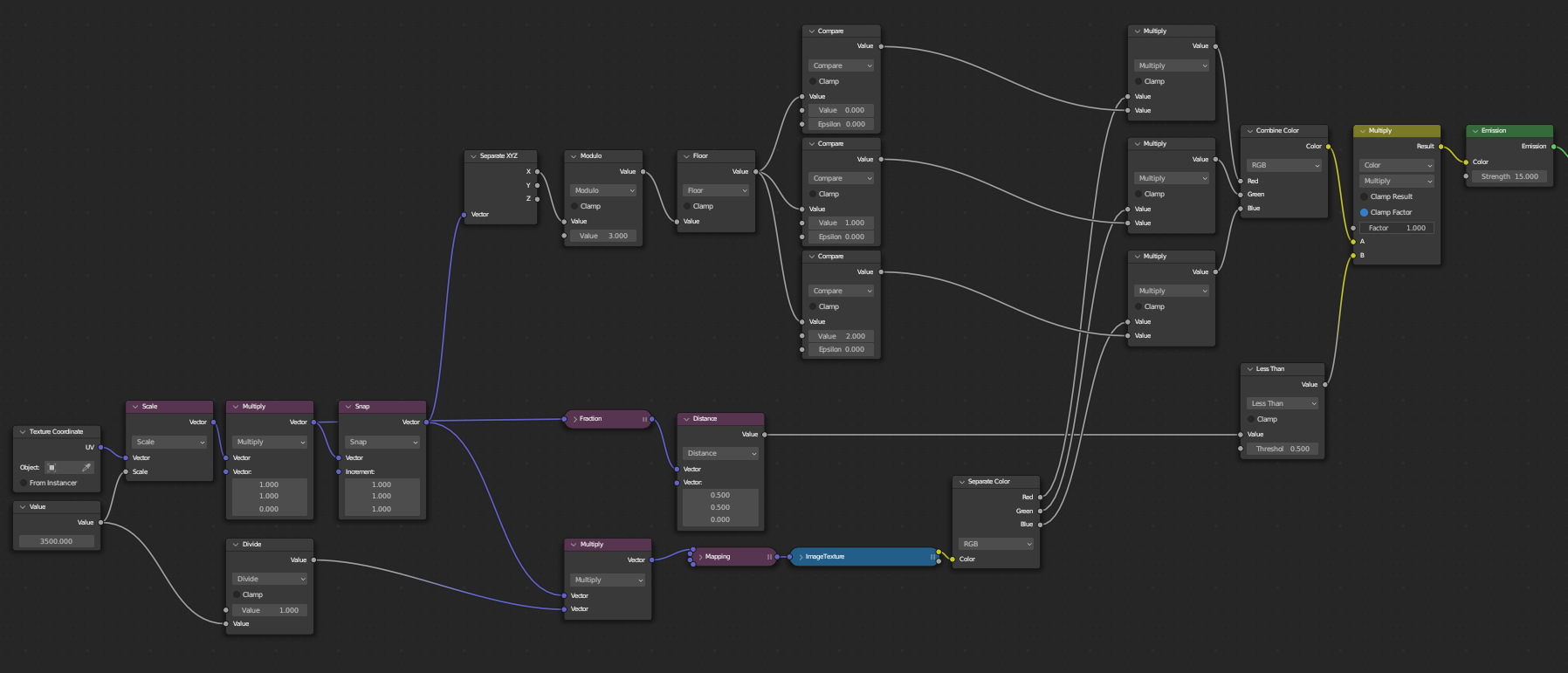
RGB Screen Shader

Please stop torturing the poor soul.

Blender Screen Shader

Programming-related

Illegal Async-to-sync pattern in JS

Don't do this.

let illegal_extraction;
Promise.resolve(':yuidumb:').then(v => { illegal_extraction = v; });

Especially Bad Parts of C++ STL

Just don't use std::regex, std::unordered_map. Please break ABI. A good drop-in replacement for std::regex is SRELL.

Google Form Endpoints

It is possible (just take a look at what requests are made) to find the Google Form submission endpoints. You can make requests directly to these, or even use it as a database with your own UI.

Monads

Every attempt to properly explain this concept is guaranteed to fail. I hope that just trying to make sense of the following example in C++ can help in some way.

#include <functional>
#include <string>
#include <iostream>

template <typename T>
class IO {
private:
    std::function<T(void)> f;
public:
    IO() = delete;
    IO(T v) : f([=](void){ return v; }) {}
    IO(const std::function<T(void)>& _f): f(_f) {}
    IO(std::function<T(void)>&& _f): f(std::move(_f)) {}

    template <typename _T>
    IO<_T> map(const std::function<_T(const T&)>& g) {
        return IO<_T>([=]() { return g(f()); });
    }

    template <typename _T>
    IO<_T> operator>>=(const std::function<IO<_T>(const T&)>& g) {
        return IO<_T>([=]() { return g(f())._Force(); });
    }

    T _Force() {
        return f();
    }
};

struct Void {};

IO<std::string> readline_IO = IO<std::string>([](){ std::string s; std::getline(std::cin, s); return s; });

std::function<IO<Void>(const std::string&)> print_IO = [](const std::string& s) {
    return IO<Void>([=](){ std::cout << s; return Void(); });
};

std::function<std::string(const std::string&)> stutter = [](const std::string& s) {
    std::string r;
    for (const char& c : s) {
        r += c;
        r += c;
    }
    return r;
};

std::function<std::string(const std::string&)> reverse = [](const std::string& s) {
    return std::string(s.crbegin(), s.crend());
};

int main() {
    auto Main = readline_IO.map(reverse).map(stutter) >>= (print_IO);

    Main._Force();
    return 0;
}

The IO monad is the original reason this concept caught on. Take note that no side effect ever occured until the call to Main._Force(). Any code utilizing IO is not supposed to call _Force. In Haskell this job is delegated to the compiler. The only other call to _Force is within the definition of operator>>=, but this is just an implementation detail as no actual side effect took place since we are just unwrapping IO<IO<T>> inside a lambda.

JS Bare Words via Proxy

Arcane magic with with. You can't make this up.

The --> operator in C

Does it even compile? One of the answer suggests this has historical importance.

Function-in-function in C++

Even not-so-dynamic languages nowadays seem to have something like this. It's still somewhat of a pain in C++. Apparently GCC has had an extension that lets you do it the way you would expect (C only):

void f() {
    void g() { /* do something */ }
    g();
}

But this somehow breaks C++ ABI apparently, so the compliant and easy way is to just write a lambda:

void f() {
    auto g = []() { /* do something*/ };
    g();
}

Recently I came across this, which I've never seen before, it's a little bit crazy:

void f() {
    struct G { static void g() { /* do something */ } };
    G::g();
}

JS await any thenable

From modderme123. What does this print? And also async is weird.

(async () => {
    let x = 0;
    const v = await ({
        then: f => {
            x=1;
            f(x);
            x=2;
        }
    })
    console.log(v,x);
})()

Also see continuations.

CSS Venetian Blinds (Animated)

For real. (Update: The magic numbers can be eliminated with new trig funcitons in CSS. Works great when you make the angle a CSS variable.) 

@keyframes bg-blinds { 
  from { background-position: 0% 0%; }
  to { background-position: 100vw 0; }
}

.vb {
  background-image: repeating-linear-gradient(15deg,
    rgba(255,255,255,.3) 0,
    rgba(255,255,255,.3) calc(100vw / 6 * 0.258819045103),
    rgba(255,255,255,.6) calc(100vw / 6 * 0.258819045103),
    rgba(255,255,255,.6) calc(100vw / 6 * 0.258819045103 * 2));
  animation: bg-blinds 10s linear infinite;
  background-size: 100vw 100%;
}

How it looks:

Hello World in Lines

This one's from KP. It uses the dark magic alternate C syntax. Make sure to compile with MSVC C++17 (x86 only). (Or g++ after removing the spaces in the <>s in the includes)

Knights of the Lambda Calculus

Supposedly, when you finish 6.001, you are to get one of those pins. These must be a collector's item now. I want one of these really bad. The one presented in the HP lectures seems to have slight variations.

AAAA

I just find it funny that when you try to swizzle the alpha into all four channels in RGBA you end up doing something like this: tex.aaaa

Building a Heap

Generally, insertion into heaps \(O(\log n)\) time. So if we want to build a heap out of \(n\) elements it would end up being \(O(n \log n)\) time. But this actually only takes \(O(n)\) time, as the insertion bound is not tight over the entire sequence of insertions. The proof is standard for introductions to data structures.

RANSAC

RANSAC is a simple method that is able to solve many chicken-or-egg problems. If we squint a little, we may even call RANSAC a sort of unsupervized learning.

Modern Machine Learning in a Nutshell

For the longest time I never understood what "AI" really meant. I thought that it was some discrete algorithm that would solve classification or even regression problems, maybe by generating decision trees efficiently. This is certainly still considered machine learning, but it's really the methods from numerical optimization that have led to the incredible results today. In short, machine learning is about finding good approximations to distributions that are either too complicated to manually model, or for which we only have limited information, and it works this way:

Mathematics-related

Limits for starters

Seeing rigour for the first time in your life, you know that in \(\mathbb R\), \(\lim_{x\to a} f(x) = L\) means: $$\forall \varepsilon > 0, \exists \delta > 0, |x-a| < \delta \implies \left|f(x) - L\right| < \varepsilon.$$ But this is hard to parse. It's easier to just think about open balls. If we introduce this notation for open intervals (intuitively a "ball" centered at \(a\)): \(B_\varepsilon(a) := (a-\varepsilon,a+\varepsilon)\), then: $$\forall \varepsilon > 0, \exists \delta > 0, x\in B_\delta(a) \implies f(x)\in B_\varepsilon(L).$$ Or even better: $$\forall \varepsilon >0, \exists \delta >0, f(B_\delta (a)) \subseteq B_\varepsilon (L)$$

(At this point it's not hard to see how this relates to the topological statement for limit points.)

Primary Decomposition of Vector Spaces (Rational Canonical Form)

We didn't spend a lot of time on this, but I think it's cool. For finite-dimensional vector space \(V\) over \(\mathbb F\) (does not even have to be closed), and let \(T \in \mathcal L(V)\), there is a decomposition: $$V=\bigoplus_i \mathcal C(q_i)$$ where \(\prod_i q_i\) is the characteristic polynomial of \(T\), and \(\mathcal C(q_i)\) denotes the subspace generated by the cyclic vector of the companion matrix for \(q_i\).

Matrix Norms

This answer is a good reference. In particular, it is shocking that for any matrix \(A \in \mathcal M_{n \times n} (\mathbb C)\): $$\sum_{i,j} |A_{i,j}|^2 = \sum_{i} s_i^2$$ where \(s_i\) are the singular values (with multiplicities).

Homonogenous Linear Recurrences

Any Fibbonacci-esque reccurence of this form: $$f(n) = \sum_{i=1}^k a_i f(n-i)$$ can be solved as an eigendecomposition problem by viewing the recurrence as a linear operation on a long vector keeping track of previous values.

Ax-Grothendieck

This is crazy. Essentially a Proof by Troll.

Riesz is currying

The low-spec version of Riesz Representation Theorem says that given \(V\) finite-dimensional inner product space, there is a one-to-one correspondence between \(V' = V \to \mathbb F\) (dual space) and linear functionals of the form \(u \mapsto \langle v,u\rangle\) for fixed \(v\). This is really just currying. Viewed as a two step process: \[V \to (V \to \mathbb F) \rightsquigarrow (V \to V) \to \mathbb F\]

Quadratic Forms and Double Integrals

If we know \(\iint_{\mathbb R^2} f(x^2 + y^2)\ dx\ dy\). Given positive symmetric \(A\in \mathcal M_{2\times 2}(\mathbb R)\), \(z=(x,y)\) and $$\iint_{\mathbb R^2} f(z^\ast Az)\ dx \ dy.$$ Use the spectral theorem to write \(A = U^\ast DU\) with \(U\) unitary, then \(z^\ast Az = (Uz)^\ast D (Uz)\), and it is clear what COV to use. Something very special happens since \(U\) is unitary.

Strange Diagram

I do not remember what this was trying to prove.

Mysterious Diagram

\(\ell^\infty\) Norm and Metric

I made a intuitive connection when I'm taking topology. The \(\ell^2\) norm
$$(x_i)_i \mapsto \sqrt{\sum_i x_i^2}$$ induces balls that are actually circles. But as you raise the \(p\) in \(\ell^p\), it becomes more and more square. (Related to how the graph of \(x \mapsto x^p\) looks.)

So naturally when you want an actual square you blow it up: \(p \to \infty\)

The \(\{0\}\) Vector Space.

Given \(V = \{0\}\), considered as a finite-dimensional vector space over field \(\mathbb F\). It comes up a bit here and there when doing linear algebra. But let's think about the vector space itself.

So next time you try to prove any statement that requires an induction on the dimension of \(V\), chances are it's a easier to set the base case at \(0 = \dim V\)!

Miscellaneous

Strange Correspondence

Math and music both involve deranged people scribbling arcane symbols in black ink on white paper.

Bezelless

The AQUOS Crystal (1 and 2) looked very ahead of their time. I still remember being a much younger soul and thinking that Shirai Kuroko's rollup phone was a crazy design.

Vision vs. Tool

This is one of the big philosophical questions I always have on my mind. It last came up when I thought about how content created pre and post the Flash era feel very different. Is it the vision that guides the tool or is it the tool that paves way for the vision? Certainly they aren't mutually exclusive but what are the specific circumstances that could cause either?

Better than TinEye

A friend (who shall remain nameless) once recalled a song that he had heard some time before. He did not remember the name but was able to recall what the music video vaguely looked like. It turns out that that was not enough information to find what the song was. Eventually he found the song by reverse-searching an AI-generated image based on his description.